二叉树（二叉搜索树）基本算法题

1.二叉树前序遍历

//递归操作
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        preorder(root, res);
        return res;
    }

    public void preorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        res.add(root.val);
        preorder(root.left, res);
        preorder(root.right, res);
    }
}
//迭代操作
//隐形的操作了一个栈
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        if (root == null) {
            return res;
        }

        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null) {
            while (node != null) {
                res.add(node.val);
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            node = node.right;
        }
        return res;
    }
}

2.二叉树的中序遍历

//递归操作
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        inorder(root, res);
        return res;
    }

    public void inorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        inorder(root.left, res);
        res.add(root.val);
        inorder(root.right, res);
    }
}
//迭代操作
![栈操作](https://img-blog.csdnimg.cn/20201108100753136.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NjY0MDIzMg==,size_16,color_FFFFFF,t_70#pic_center)
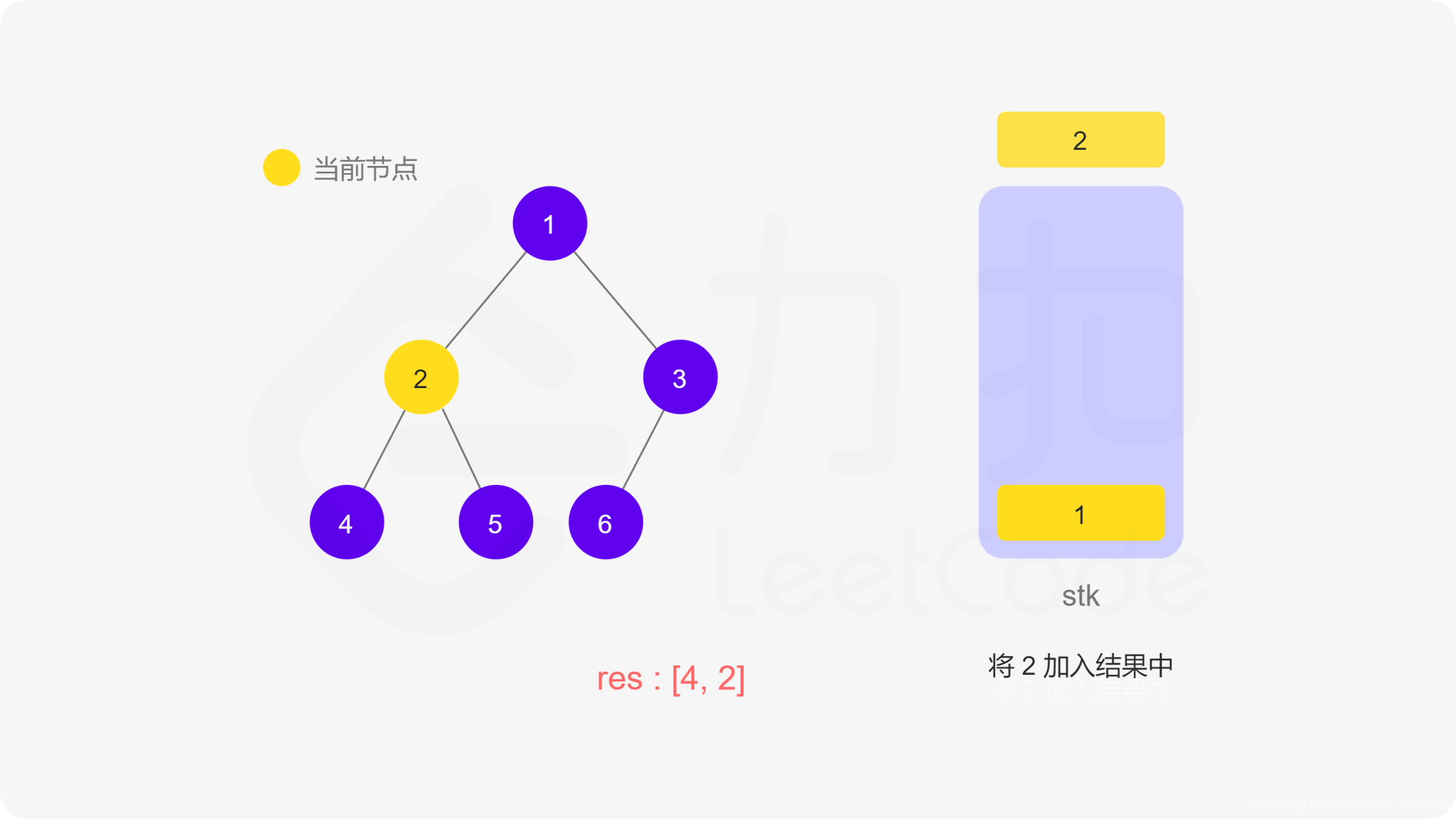
[中序遍历](https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/er-cha-shu-de-zhong-xu-bian-li-by-leetcode-solutio/)
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        Deque<TreeNode> stk = new LinkedList<TreeNode>();
        while (root != null || !stk.isEmpty()) {
            while (root != null) {
                stk.push(root);
                root = root.left;
            }
            root = stk.pop();
            res.add(root.val);
            root = root.right;
        }
        return res;
    }
}
3.二叉树后序遍历
//递归操作
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        postorder(root, res);
        return res;
    }

    public void postorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        postorder(root.left, res);
        postorder(root.right, res);
        res.add(root.val);
    }
}
/迭代操作
[后序遍历](https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/er-cha-shu-de-hou-xu-bian-li-by-leetcode-solution/)
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        if (root == null) {
            return res;
        }
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode prev = null;
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if (root.right == null || root.right == prev) {
                res.add(root.val);
                prev = root;
                root = null;
            } else {
                stack.push(root);
                root = root.right;
            }
        }
        return res;
    }
}
4.二叉树的广度优先搜索（层序遍历BFS）
[层序遍历](https://leetcode-cn.com/problems/binary-tree-level-order-traversal/solution/er-cha-shu-de-ceng-xu-bian-li-by-leetcode-solution/)
队列先进先出，栈先进后出
队列（头部插入，尾部删除）实现的类是LinkedList（双向链表）
常用方法：
add(E e) 将指定的元素插入此队列（如果立即可行且不会违反容量限制），
在成功时返回 true，如果当前没有可用的空间，则抛出 IllegalStateException。
element() 获取，但是不移除此队列的头。
offer(E e) 将指定的元素插入此队列（如果立即可行且不会违反容量限制），
当使用有容量限制的队列时，此方法通常要优于 add(E)，
后者可能无法插入元素，而只是抛出一个异常。
peek() 获取但不移除此队列的头；如果此队列为空，则返回 null。
poll() 获取并移除此队列的头，如果此队列为空，则返回 null。
remove() 获取并移除此队列的头。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ret = new ArrayList<List<Integer>>();
        if (root == null) {
            return ret;
        }

        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> level = new ArrayList<Integer>();
            int currentLevelSize = queue.size();
            for (int i = 1; i <= currentLevelSize; ++i) {
                TreeNode node = queue.poll();
                level.add(node.val);
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            ret.add(level);
        }
        
        return ret;
    }
}
5.树的最大深度
递归实现
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftHeight = maxDepth(root.left);
            int rightHeight = maxDepth(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}
迭代实现（广度优先搜索）
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        int ans = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size > 0) {
                TreeNode node = queue.poll();
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
                size--;
            }
            ans++;
        }
        return ans;
    }
}
6.对称二叉树
[对称二叉树](https://leetcode-cn.com/problems/symmetric-tree/solution/dui-cheng-er-cha-shu-by-leetcode-solution/)
递归实现
class Solution {
    public boolean isSymmetric(TreeNode root) {
          return check(root,root);      
        }
        public boolean check(TreeNode p,TreeNode q){
            if(p == null && q == null){
                return true;
            }else if(p == null || q == null){
                return false;
            }else {
                return p.val == q.val && check(p.left,q.right) && check(p.right,q.left);
            }
        }
    }
    非递归实现
    class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root, root);
    }

    public boolean check(TreeNode u, TreeNode v) {
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.offer(u);
        q.offer(v);
        while (!q.isEmpty()) {
            u = q.poll();
            v = q.poll();
            if (u == null && v == null) {
                continue;
            }
            if ((u == null || v == null) || (u.val != v.val)) {
                return false;
            }

            q.offer(u.left);
            q.offer(v.right);

            q.offer(u.right);
            q.offer(v.left);
        }
        return true;
    }
}
7.路径总和
广度优先搜素
[二叉树路总和](https://leetcode-cn.com/problems/path-sum/solution/lu-jing-zong-he-by-leetcode-solution/)
class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        Queue<TreeNode> queNode = new LinkedList<TreeNode>();
        Queue<Integer> queVal = new LinkedList<Integer>();
        queNode.offer(root);
        queVal.offer(root.val);
        while (!queNode.isEmpty()) {
            TreeNode now = queNode.poll();
            int temp = queVal.poll();
            if (now.left == null && now.right == null) {
                if (temp == sum) {
                    return true;
                }
                continue;
            }
            if (now.left != null) {
                queNode.offer(now.left);
                queVal.offer(now.left.val + temp);
            }
            if (now.right != null) {
                queNode.offer(now.right);
                queVal.offer(now.right.val + temp);
            }
        }
        return false;
    }
}
递归
class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        if (root.left == null && root.right == null) {
            return sum == root.val;
        }
        return hasPathSum(root.left, sum - root.val) || 
        hasPathSum(root.right, sum - root.val);
 8.从中序遍历后序遍历构造二叉树
 递归算法
 [构造二叉树](https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solution/cong-zhong-xu-yu-hou-xu-bian-li-xu-lie-gou-zao-14/)

```go

```java
 class Solution {
    int post_idx;
    int[] postorder;
    int[] inorder;
    Map<Integer, Integer> idx_map = new HashMap<Integer, Integer>();

    public TreeNode helper(int in_left, int in_right) {
        // 如果这里没有节点构造二叉树了，就结束
        if (in_left > in_right) {
            return null;
        }

        // 选择 post_idx 位置的元素作为当前子树根节点
        int root_val = postorder[post_idx];
        TreeNode root = new TreeNode(root_val);

        // 根据 root 所在位置分成左右两棵子树
        int index = idx_map.get(root_val);

        // 下标减一
        post_idx--;
        // 构造右子树
        root.right = helper(index + 1, in_right);
        // 构造左子树
        root.left = helper(in_left, index - 1);
        return root;
    }

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        this.postorder = postorder;
        this.inorder = inorder;
        // 从后序遍历的最后一个元素开始
        post_idx = postorder.length - 1;

        // 建立（元素，下标）键值对的哈希表
        int idx = 0;
        for (Integer val : inorder) {
            idx_map.put(val, idx++);
        }
        
        return helper(0, inorder.length - 1);
    }
}
9.填充每个节点的下一个右侧节点指针
层次遍历
class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return root;
        }
        
        // 初始化队列同时将第一层节点加入队列中，即根节点
        Queue<Node> queue = new LinkedList<Node>(); 
        queue.add(root);
        
        // 外层的 while 循环迭代的是层数
        while (!queue.isEmpty()) {
            
            // 记录当前队列大小
            int size = queue.size();
            
            // 遍历这一层的所有节点
            for (int i = 0; i < size; i++) {
                
                // 从队首取出元素
                Node node = queue.poll();
                
                // 连接
                if (i < size - 1) {
                    node.next = queue.peek();
                }
                
                // 拓展下一层节点
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
            }
        }
        
        // 返回根节点
        return root;
    }
}
[当有一个节点为null时](https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node-ii/solution/tian-chong-mei-ge-jie-dian-de-xia-yi-ge-you-ce-15/)
class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return null;
        }
        Queue<Node> queue = new LinkedList<Node>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int n = queue.size();
            Node last = null;
            for (int i = 1; i <= n; ++i) {
                Node f = queue.poll();
                if (f.left != null) {
                    queue.offer(f.left);
                }
                if (f.right != null) {
                    queue.offer(f.right);
                }
                if (i != 1) {
                    last.next = f;
                }
                last = f;
            }
        }
        return root;
    }
}
10.二叉树的公共祖先
[二叉树的公共祖先](https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/solution/er-cha-shu-de-zui-jin-gong-gong-zu-xian-by-leetc-2/)
递归算法（后续遍历）
递归解析：
终止条件：
当越过叶节点，则直接返回 null ；
当 root 等于 p, q ，则直接返回 root ；
递推工作：
开启递归左子节点，返回值记为 left；
开启递归右子节点，返回值记为 right ；
返回值： 根据 left和 right ，可展开为四种情况；
当 left 和 right 同时为空 ：
说明 root的左 / 右子树中都不包含 p,qp,q ，返回 null ；
当 left和 right 同时不为空 ：
说明 p, qp,q 分列在 rootroot 的 异侧 （分别在 左 / 右子树），因此 rootroot 为最近公共祖先，返回 rootroot ；
当 leftleft 为空 ，rightright 不为空 ：
p,qp,q 都不在 rootroot 的左子树中，直接返回 rightright 。具体可分为两种情况：
p,qp,q 其中一个在 rootroot 的 右子树 中，此时 rightright 指向 pp（假设为 pp ）；
p,qp,q 两节点都在 rootroot 的 右子树 中，此时的 rightright 指向 最近公共祖先节点 ；
当 leftleft 不为空 ， rightright 为空 ：与情况 3. 同理
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || root == p || root == q) return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if(left == null && right == null) return null; // 1.
        if(left == null) return right; // 3.
        if(right == null) return left; // 4.
        return root; // 2. if(left != null and right != null)
    }
}
11.二叉树的序列化与反序列化
[序列化与反序列化](https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree/solution/er-cha-shu-de-xu-lie-hua-yu-fan-xu-lie-hua-by-le-2/)
1）和 String 类不同的是，StringBuffer 和 StringBuilder 类的对象能够被多次的修改，
并且不产生新的未使用对象。
2）StringBuilder 和 StringBuffer 之间的最大不同在于 StringBuilder 的方法
不是线程安全的（不能同步访问）。
3）由于 StringBuilder 相较于 StringBuffer 有速度优势，
所以多数情况下建议使用 StringBuilder 类。然而在应用程序要求线程安全的情况下，
则必须使用 StringBuffer 类。
public class Codec {
    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if (root == null) {
            return "";
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        StringBuffer res = new StringBuffer();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode curNode = queue.poll();
            if (curNode != null) {
                res.append(curNode.val+",");
                queue.offer(curNode.left);
                queue.offer(curNode.right);
            } else {
                res.append("null,");
            }
        } 
        return res.toString();
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        if (data=="") {
            return null;
        }
        String[] val = data.substring(0, data.length() - 1).split(",");
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        TreeNode root = new TreeNode(Integer.parseInt(val[0]));
        int cur = 1;
        queue.offer(root);
        while (!queue.isEmpty()) { 
            TreeNode curNode = queue.poll();
            if (!"null".equals(val[cur])){
                curNode.left = new TreeNode(Integer.valueOf(val[cur]));
                queue.offer(curNode.left);
            }
            cur++; 
            if (!"null".equals(val[cur])) {
                curNode.right = new TreeNode(Integer.valueOf(val[cur]));
                queue.offer(curNode.right);
            }
            cur++;
        }
        return root;
    }
}
12.二叉搜索树（中序遍历一定是升序的)
二叉搜索树（BST）是二叉树的一种特殊表示形式，它满足如下特性：
每个节点中的值必须大于（或等于）存储在其左侧子树中的任何值。
每个节点中的值必须小于（或等于）存储在其右子树中的任何值。
[二叉搜索树](https://leetcode-cn.com/problems/validate-binary-search-tree/solution/yan-zheng-er-cha-sou-suo-shu-by-leetcode-solution/)
//中序遍历
class Solution {
    public boolean isValidBST(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        double inorder = -Double.MAX_VALUE;
        while (!stack.isEmpty() || root != null) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
 . 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树
            if (root.val <= inorder) {
                return false;
            }
            inorder = root.val;
            root = root.right;
        }
        return true;
    }
}
13.二叉搜索树迭代器
[二叉搜索树迭代器](https://leetcode-cn.com/problems/binary-search-tree-iterator/solution/er-cha-sou-suo-shu-die-dai-qi-by-leetcode/)
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode(int x) { val = x; }
 * }
 */
 初始化一个空数组用来存放二叉搜索树的中序序列。
我们按中序遍历二叉搜索树，按照左中右的顺序处理节点。
一旦所有节点都在数组中，则我们只需要一个指针或索引来实现 next() 和 hasNext 这两个函数。
每当调用 hasNext() 时，我们只需要检查索引是否达到数组末尾。
每当调用 next() 时，我们只需要返回索引指向的元素，并向前移动一步，以模拟迭代器的进度。

class BSTIterator {

    ArrayList<Integer> nodesSorted;
    int index;

    public BSTIterator(TreeNode root) {

        // Array containing all the nodes in the sorted order
        this.nodesSorted = new ArrayList<Integer>();
        
        // Pointer to the next smallest element in the BST
        this.index = -1;
        
        // Call to flatten the input binary search tree
        this._inorder(root);
    }

    private void _inorder(TreeNode root) {

        if (root == null) {
            return;
        }

        this._inorder(root.left);
        this.nodesSorted.add(root.val);
        this._inorder(root.right);
    }

    /**
     * @return the next smallest number
     */
    public int next() {
        return this.nodesSorted.get(++this.index);
    }

    /**
     * @return whether we have a next smallest number
     */
    public boolean hasNext() {
        return this.index + 1 < this.nodesSorted.size();
    }
}
14.二叉搜索树查找元素
递归实现
class Solution {
  public TreeNode searchBST(TreeNode root, int val) {
    if (root == null || val == root.val) return root;

    return val < root.val ? searchBST(root.left, val) : searchBST(root.right, val);
  }
}
迭代实现
class Solution {
  public TreeNode searchBST(TreeNode root, int val) {
    while (root != null && val != root.val)
      root = val < root.val ? root.left : root.right;
    return root;
  }
}
15.二叉搜索树查找元素
递归
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }

        if (val < root.val) {
            root.left = insertIntoBST(root.left, val);
        } else {
            root.right = insertIntoBST(root.right, val);
        }
        return root;
    }
}
思路与算法

首先回顾二叉搜索树的性质：对于任意节点 \textit{root}root 而言，
左子树（如果存在）上所有节点的值均小于 \textit{root.val}root.val，
右子树（如果存在）上所有节点的值均大于 \textit{root.val}root.val，
且它们都是二叉搜索树。因此，当将 \textit{val}val 插入到以 \textitroot 为根的子树上时，根据 \textit{val}val 与 \textit{root.val}root.val 的大小关系，
就可以确定要将 \textit{val}val 插入到哪个子树中。
如果该子树不为空，则问题转化成了将 \textit{val}val 插入到对应子树上。
否则，在此处新建一个以 \textit{val}val 为值的节点，
并链接到其父节点 \textit{root}root 上。
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }
        TreeNode pos = root;
        while (pos != null) {
            if (val < pos.val) {
                if (pos.left == null) {
                    pos.left = new TreeNode(val);
                    break;
                } else {
                    pos = pos.left;
                }
            } else {
                if (pos.right == null) {
                    pos.right = new TreeNode(val);
                    break;
                } else {
                    pos = pos.right;
                }
            }
        }
        return root;
    }
}
16.二叉搜索树插入元素
递归解法
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }

        if (val < root.val) {
            root.left = insertIntoBST(root.left, val);
        } else {
            root.right = insertIntoBST(root.right, val);
        }
        return root;
    }
}
首先回顾二叉搜索树的性质：对于任意节点 root 而言，
左子树（如果存在）上所有节点的值均小于root.val，
右子树（如果存在）上所有节点的值均大于root.val，且它们都是二叉搜索树。
因此，当将 val 插入到以root 为根的子树上时，根据val 与 root.val 的大小关系，
就可以确定要将 val 插入到哪个子树中。
如果该子树不为空，则问题转化成了将val 插入到对应子树上。
否则，在此处新建一个以val 为值的节点，并链接到其父节点root 上。。
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }
        TreeNode pos = root;
        while (pos != null) {
            if (val < pos.val) {
                if (pos.left == null) {
                    pos.left = new TreeNode(val);
                    break;
                } else {
                    pos = pos.left;
                }
            } else {
                if (pos.right == null) {
                    pos.right = new TreeNode(val);
                    break;
                } else {
                    pos = pos.right;
                }
            }
        }
        return root;
    }
}
***17.二叉搜索树删除节点
[删除节点](https://leetcode-cn.com/problems/delete-node-in-a-bst/solution/shan-chu-er-cha-sou-suo-shu-zhong-de-jie-dian-by-l/)
class Solution {
  /*
  One step right and then always left
  */
  public int successor(TreeNode root) {
    root = root.right;
    while (root.left != null) root = root.left;
    return root.val;
  }

  /*
  One step left and then always right
  */
  public int predecessor(TreeNode root) {
    root = root.left;
    while (root.right != null) root = root.right;
    return root.val;
  }

  public TreeNode deleteNode(TreeNode root, int key) {
    if (root == null) return null;
    if (key > root.val) root.right = deleteNode(root.right, key);
    else if (key < root.val) root.left = deleteNode(root.left, key);
    else {
      if (root.left == null && root.right == null) root = null;
      else if (root.right != null) {
        root.val = successor(root);
        root.right = deleteNode(root.right, root.val);
      }
      else {
        root.val = predecessor(root);
        root.left = deleteNode(root.left, root.val);
      }
    }
    return root;
  }
}
18.数据流中第k大的元素
[力扣](https://leetcode-cn.com/problems/kth-largest-element-in-a-stream/)
19.二叉搜索树的最近公共祖先（力扣235）
一次遍历
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root,
     TreeNode p, TreeNode q) {
        TreeNode ancestor = root;
        while (true) {
            if (p.val < ancestor.val && q.val < ancestor.val) {
                ancestor = ancestor.left;
            } else if (p.val > ancestor.val && q.val > ancestor.val) {
                ancestor = ancestor.right;
            } else {
                break;
            }
        }
        return ancestor;
    }
}
两次遍历
List的方法：
add（）将元素添加到链表的尾部
add（index，e）在指定位置添加元素
get（index）检查指定索引的元素并返回
indexof（）返回链表中的索引
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root,
     TreeNode p, TreeNode q) {
        List<TreeNode> path_p = getPath(root, p);
        List<TreeNode> path_q = getPath(root, q);
        TreeNode ancestor = null;
        for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) {
            if (path_p.get(i) == path_q.get(i)) {
                ancestor = path_p.get(i);
            } else {
                break;
            }
        }
        return ancestor;
    }
    public List<TreeNode> getPath(TreeNode root, TreeNode target) {
        List<TreeNode> path = new ArrayList<TreeNode>();
        TreeNode node = root;
        while (node != target) {
            path.add(node);
            if (target.val < node.val) {
                node = node.left;
            } else {
                node = node.right;
            }
        }
        path.add(node);
        return path;
    }
}

本文地址：https://blog.csdn.net/weixin_46640232/article/details/109545264