背景

在目前常见的交互方式中，动画扮演了一个重要的角色。

在 Weex 框架下，Weex 的动画需要屏蔽 CSS/JS 动画与 Android 动画系统的差异，并尽可能的达到60FPS。

本文阐述了在 Android 上实现高性能CSS/JS动画过程中所遇到的问题/相关数学知识及解决方案。本文使用的前端 DSL 为 Weex vue 1.0或 Weex Vue 2.0。

现状与问题

在 Weex 环境下，一个典型的动画在前端DSL中的写法如下:

animation = weex.requireModule('animation')
animation.transition(testEl, {
    styles: {
        color: '#FF0000',
        transform: 'translate(250px, 100px) rotate(60deg)',
        transformOrigin: 'center center'
    },
    duration: 800, //ms
    timingFunction: 'ease',
    delay: 0 //ms
    }, function () {
        modal.toast({ message: 'animation finished.' })
})

对于上述代码片段，Weex Android需要处理下述问题。

transform 字段的解析

为了符合传统意义上的前端的书写习惯，transform 字段没有使用JSON表示，而是使用了一个字符串表示。在 transform 里，逗号前后可能没有空格，也可能有多个空格，transform里的函数名称和参数的数据类型也不确定，且面临后期需求变更的可能性。

对于复杂字符串的解析与处理，常见的方式是正则表达式。然而在此场景下使用正则表达式，面临如下困难：

正则表达式在 Android 下性能较差，对于每秒60帧，每帧对数百个元素做动画的场景，正则表达式将会成为整个动画模块的性能瓶颈。
正则表达式的可维护性很差，对于需求变更很不友好，经过需求变更及人员调整后，复杂的正则表达式往往无法维护，只能推导重写。

Android 动画方案的选择

在Android系统层面，存在Property Animation, View Animation, Drawable Animation三种动画体系，且三个体系互不兼容。Weex需要选择一个动画体系达到以下目的：

将前端指定的 styles(如transform，color)和 timing-function 以合理的方式映射到 Android 端。
style 和 timing-function 对修改友好。
可以使用 Android 手机的 GPU 能力提高动画帧率。

3D动画的实现

支持 rotateX, rotateY 属性，实现如下的 3d 动画效果：

Weex Android 动画揭秘

方案

针对上面的问题，分别使用下述方案进行优化。

解析 transform

为了应对 transform 字段的变化并提高解析性能，Weex 使用了 LL Parser 的方式来解析 transform 字段。

形式文法

LL Parser是一种解析形式语言的方式。按照Chomsky hierarchy，形式语言的表达能力从弱到强可划分为下面4类:

Regular Grammars，如正则表达式，缺陷是无法表达递归这个概念。
Context-free Grammars，如 Java/C/Python 等常见的编程语言。
Context-sensitive Grammars，如HTML，同 Java/C/Python 相比，Context-sensitive Grammars 允许 HTML 支持下面的语法：对于标签<a>，无论是否存在对应的闭标签</a>，均符合语法。
Recursively enumerable Grammars，图灵机识别形式语言的能力上限，一般只存在于理论中。

可以将形式语言中的符号的划分为下面两类，终结符号和非终结符号，下面使用EBNF的方式，给出了整数(integer)在形式语言中的定义。在这个定义中，integer和digit是非终结符，双引号中的0,1,2,3,4,5,6,7,8,9,-均为终结符号。非终结符号可以由推导规则进行推导，而终结符号则无法进行推导。

integer = ["-"], digit, {digit} ;
digit =  "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" ;

在更复杂的推导规则中，非终结符可以被递归推导。

LL Parser

LL Parser 是一种解析Context-free Grammars的方式。在常见的编程语言中实现 LL Parser 时，一般会把非终结符号用该语言中的函数表示，Context-free Grammar中的递归可以映射为编程语言中函数的递归；终结符号则一般使用字符串处理技术来处理。

transform 的定义、解析及扩展

对于transform，用下述 ENBF 形式进行定义:

  definition = {function};
  function = name, "(", value, { ",", value } , ")";
  name = character, {character};
  value = identifier, {identifier};
  identifier = character | "." | "%" | "+" | "-";
  character = digit | letter;
  digit =  "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" ;
  letter = "A" | "B" | "C" | "D" | "E" | "F" | "G"
       | "H" | "I" | "J" | "K" | "L" | "M" | "N"
       | "O" | "P" | "Q" | "R" | "S" | "T" | "U"
       | "V" | "W" | "X" | "Y" | "Z" | "a" | "b"
       | "c" | "d" | "e" | "f" | "g" | "h" | "i"
       | "j" | "k" | "l" | "m" | "n" | "o" | "p"
       | "q" | "r" | "s" | "t" | "u" | "v" | "w"
       | "x" | "y" | "z" ;

Weex 对 transform 解析的解析使用了 LL Parser 的方式，代码参见 FunctionParser。

实际上，使用上述文法，不仅定义了 transform, 还定义了 rgb(244, 23, 400) 等模式。所以上述 FunctionParser 具有较强的通用性，不仅适用于 transform ，还可以应用于其他字段上。

动画方案的选择

Android在系统层面，提供了三种动画机制，分别是 Drawable Animation, View Animation, Property Animation.

Drawable Animation 与 View Animation

Drawable Animation最简单，但一般用于动画类型和持续时间已经在编译时确定的场景，并不适用于 Weex 这样的动态化方案。

View Animation 的复杂度适中，但扩展性差，只能将动画应用于下述View的属性上:

rotate
scale
translate
alpha

基于扩展性考虑，Weex 的动画方案选择了 Property Animation。

Property Animation

在狭义上，动画可以被视为为某个对象的一个或多个属性随着时间变化的过程。动画的这种表示形式与数学上的函数很相似，在Android中，可以用如下函数描述Property Animation:

Weex Android 动画揭秘

公式中变量的意义如下：

t，a^T, b^T 分别代表时间序列、属性起始值序列、属性终止值序列，三者均为向量。函数*生了一个 n * m 的矩阵
t_j 为指定的时间点，a_i 为动画起始时某个属性的值，b_i为动画终止时某个属性的值。

下面具体阐述上面的函数。

ObjectAnimator

在Android中，每一次屏幕刷新，会产生一个 VSync 硬件中断。当系统收到 VSync时，会调用Choreographer的回调函数，在回调函数中，ObjectAnimator会被触发。

ObjectAnimator首先根据当前的硬件时钟，确定t_j的取值，之后求出该时间点对应的列向量。然后根据列向量中每一行的取值，依次更新对应的属性。

因此，t_j可以视为插值时间，插值时间序列 t 与属性变换函数序列 g 的外积为函数G，即ObjectAnimator。

由于Choreographer的回调函数每一次被调用，可以确定一个t_j，故t_j是离散的，所以 t 是一个离散变量，G是一个离散函数。

TypeEvaluator 与 Property

当ObjectAnimator依次更新对象的属性时，由于Java语言缺少函数指针的概念，ObjectAnimator无法更新复杂的属性值，只能对基本数据类型进行更新。

为了解决这个问题，可以使用 Property 对复杂对象的setter/getter进行封装，ObjectAnimator使用封装后的 Property 即可完成复杂属性的更新操作。

对于下面的这些属性，如果使用Property的方式更新它们的值，Android系统将自动启用 GPU 硬件加速：

rotate
rotateX
rotateY
scaleX
scaleY
translateX
translateY
alpha

当面对需求变更，需要增加新的属性时，编写新的 Property 即可。

函数g_i是插值时间、起始值、终止值三个变量的函数，在Android 中，用TypeEvaluator 表示 g_i。ObjectAnimator 会使用 TypeEvaluator 的值来更新对应的 Property。

g_i可能为非单调函数，下图为一个弹跳效果的函数曲线，a，b为某个确定的值，f(t_j)为x轴，表示插值时间；g_i为y轴，表示物体在弹跳方向上的高度：

Weex Android 动画揭秘

TimeInterpolator

在经典物理学中，时间是一个单调的线性函数。但在动画场景下，一些变化可能是非线性乃至非单调的，例如加速运动或弹跳效果。

函数f_j在 Property Animations 中以 TimeInterpolator 的形式存在，可以视其为一个篡改时间的函数。通过这个函数，可以把物理上的真实时间映射到[0,1]区间上，映射后的值表示动画完成的比例。下图展示了函数f_j的几种可能情况。

Weex Android 动画揭秘

在Weex Android的动画中，transform/style 被映射到了TypeEvaluator上，仍使用简单的线性函数；timing-function 映射到了 TimeInterpolator 上，该函数可能为来实现非单调函数，如 Bézier_curve。

3D Animation

目前 Weex 的 3D Animation特指 rotateX, rotateY, perspective 这三个属性，前端可以利用这三个属性实现一些3D效果。

Mathematics

下面首先阐述动画在2D空间上遇到的一些数学问题及解决方案，之后再扩展到3D空间。

2D Linear Transformation

2D空间上的点可以视为一个2维向量空间上的向量。rotate，scale 可以视为线性变换(Linear Transformation)矩阵。

当该矩阵是单位矩阵，点P(x,y)仍然保持原座标不变，如下图所示：

Weex Android 动画揭秘

该矩阵对角线上的值表示scale，下图中的线性变换将点P(x,y)的座标放到大了3/2倍:

Weex Android 动画揭秘

对于rotate，可以用下图的线性变换表示：

Weex Android 动画揭秘

使用线性变换表示 rotate, scale有两个优点：

可以方便的对物体进行上述变换，下图中等式左边第一个矩阵仍表示线性变换，等式左边第二个矩阵表示图中白色五边形的顶点，通过下面的矩阵乘法，可以轻松将原物体放大至3/2倍(白色物体变为黄色物体)。
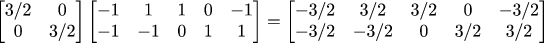```
![](https://raw.githubusercontent.com/ssloy/tinyrenderer/gh-pages/img/04-perspective-projection/f03.png)

![](https://raw.githubusercontent.com/ssloy/tinyrenderer/gh-pages/img/04-perspective-projection/2aa8b671e124f1511c3b47a37c47f150.png)
```
由于多个线性变换可以用乘法相连接，因此用一个矩阵就可以表示多个线性变换。对于有数十万乃至数百万个顶点的物体，进行数十个线性变换后，求物体顶点座标的问题，可以简化乘两个矩阵相乘问题，这样在计算时间和存储空间消耗上都有很大节省。

2D Affine Transformation 与 Homogeneous coordinates

然而，translation 并不是一个线性变换，当需要为二维向量做 translation 时，在2维向量空间中只能使用加法实现，即如下图所示：

Weex Android 动画揭秘

当数十个矩阵加法/乘法混合后，计算复杂度和空间复杂度相比之前的线性变换都会有显著增加，数学形式上也会变得很复杂。下图所示的矩阵运算仅表示两个线性变换和一个 translation 组合的情况，计算已经很复杂，当变换数量和顶点数量增加后，形式会变得更加复杂。

Weex Android 动画揭秘

2D translation在二维向量空间上其实是一个 Affine Transformation ，即一个线性变换连接上一个向量平移，形式如下图所示：

Weex Android 动画揭秘

为了将上述 Affine Transformation 转变为Linear Transformation ，在计算机图形学中经常在3D Homogeneous coordinates 下表示2D空间上的点。

对于m维向量空间上的 Affine Transformation，可以通过添加一个额外的维度，转变为m+1维上的Linear Transformation，m+1的向量空间被称为 Homogeneous coordinates 。

由于2D空间内的 translation, rotate, scale 均是二维向量空间内的 Affine Transformation，因此在3D Homogeneous coordinates 下，上述变换将变为 Linear Transformation.

下面的例子中为点 P(x,y) 增加了一个额外的维度后(即点 P 位于平面z=1上)，使用线性变换即可完成translation，亦将点 P(x,y) 移动到点 P(x+3, y+2)。

Weex Android 动画揭秘

Projection

对于3D建模后生成的物体而言，由于目前手机屏幕是二维的，观察者最终看到的是三维空间的物体在二维屏幕上的投影。

常见的投影方式有两种，Parallel Projection 和 Perspective Prjection，下面将详细介绍。

Parallel Projection

Parallel Projection又可分为两种，Orthographic Projection 和 Oblique Projection:

下面为 Orthographic Projection，投影线与投影平面垂直:

Weex Android 动画揭秘

下图为Oblique Projection，投影线与投影平面不垂直，存在一定的夹角:

Weex Android 动画揭秘

无论哪种情况，在Parallel Projection中，投影线之间总是相互平行。

Perspective Projection

在Perspective Projection中，投影线聚焦于一点，该点被称为Vanishing Point。

Weex Android 动画揭秘

Perspective Projection 同 Parallel Projection 相比，更符合人眼对现实世界的观察，离观察者近的物体看起来大，离观察者远的物体看起来小，下图展示了Perspective Projection中的一些基本概念:

Weex Android 动画揭秘

观察者(viewer)或 Camera，即图中的人眼。由于所有的光线汇聚于人眼，因此人眼所在位置是 Vanishing Point。
Objects，图中虚线圆，即被投影的物体。
Projection Plane，即图中的 Drawing Surface，物体将会被投影到此平面上。观察者看不到Object，只能看到 Object 在 Projection Plane 上的投影。
图中的d是观察者离投影平面的距离，d越大时，投影线之间的夹角越小，投影效果越接近于Orthographic Projection。当d为正无穷时，投影线之间互相平行，此时Perspective Projection 变成了 Orthographic Projection。因此Orthographic Projection是Perspective Projection的一个特例。

在一个典型3D渲染模型中，Projection Plane一般为屏幕，Camera为开发者设置的一个点，Objects是开发者对于物体的建模，用户最终只能看到 Objects 在屏幕上的投影。

Implementation

在Weex中，开发者可以通过设置 rotateX、rotateY 获得 Perspective Projection 的效果，使用 perspective 属性控制 Camera 到 Projection Plane的距离，当不设置 perspective 时，weex 会把 perspective 设置为正无穷，以达到 Orthographic Projection 的效果。

效果展示

经过上述多种方案的协同优化，Weex动画的帧率同未优化(未使用 Parser, GPU)时相比，得到了极大的提升。

优化前的帧率和动画效果如下，可以看到运行一段时间后，每帧渲染时间远大于17ms：

Weex Android 动画揭秘

优化后的帧率和动画效果如下，保长期运行后，每帧渲染时间依然保持在17ms左右，动画无明显卡顿：

Weex Android 动画揭秘

下图展示了 3D rotation 的效果，关键代码片段如下，可以看到由于 perspective 属性的存在，图片呈现出了 离观察者近的部分较大，离观察者远的部分较小 的效果，目前 perspective 只在 Weex 0.16 以上支持：

animation.transition(testEl, {
    styles: {
        color: '#FF0000',
        transform: 'rotateY(45deg) perspective(1800px)',
        transformOrigin: 'center center'
        },
    duration: 3000, //ms
    timingFunction: 'ease',
    delay: 0 //ms
    }, 
    function () {
        modal.toast({ message: 'animation finished.' })
})

Weex Android 动画揭秘

Weex Android 动画揭秘

背景

现状与问题

transform 字段的解析

Android 动画方案的选择

3D动画的实现

方案

解析 transform

形式文法

LL Parser

transform 的定义、解析及扩展

动画方案的选择

Drawable Animation 与 View Animation

Property Animation

ObjectAnimator

TypeEvaluator 与 Property

TimeInterpolator

3D Animation

Mathematics

2D Linear Transformation

2D Affine Transformation 与 Homogeneous coordinates

Projection

Parallel Projection

Perspective Projection

Implementation

效果展示

参考资料

Weex Android 动画揭秘

android weex 环境安装笔记windows环境

weex android 基础与扩展本地图片加载 gif播放自定义module

weex sdk集成到Android工程三. weex服务项目搭建

Weex基于Android Studio从开发环境搭建到运行

weex sdk集成到Android工程一. 阿里Weex框架快速体验与环境搭建

Android技能树 — 动画小结

Android动画效果之自定义ViewGroup添加布局动画（五）

Android自定义加载loading view动画组件

Android实现跳动的小球加载动画效果