机器学习算法总结

线性回归

利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间的关系进行建模的一种分析方式

线性回归主要有两种模型 线性关系 非线性关系

1. sklearn.linear_model.LinearRegression()

   • ​ LinearRegression.coef_：回归系数

2. 线性回归的损失和优化

损失函数

• yi为第i个训练样本的真实值
• h(xi)为第i个训练样本特征值组合预测函数
• 又称最小二乘法

3. 优化算法

   两种优化算法:

   • 正规方程

理解:X为特征值矩阵，y为目标值矩阵。直接求到最好的结果

 缺点:当特征过多过复杂时，求解速度太慢并且得不到结果

​

​ 正规方程的推到过程

​ 其中y是真实值矩阵，X是特征值矩阵，w是权重矩阵

对其求解关于w的最小值，起止y,X 均已知二次函数直接求导，导数为零的位置，即为最小值。

• 梯度下降

  
  α: 学习率 可以理解成每次求导的步长

• 梯度的概念

  • 单变量 – 切线
  • 多变量 – 向量

• ​

  梯度下降	正规方程
  需要选择学习率	不需要
  需要迭代求解	一次运算得出
  特征数量较大可以使用	需要计算方程,时间复杂度高

  • 小数据量 正规方程(不能解决你和问题) 岭回归
  • 大数据量 梯度下降

• 全梯度下降算法(FG)

  • 对所有训练样本的误差,对其求和再取平均值作为目标函数

• 随机梯度下降算法(SG)

  • 每次只代入计算一个样本目标函数的梯度来更新权重，再取下一个样本重复此过程，直到损失函数值停止下降或损失函数值小于某个可以容忍的阈值

   其中，x(i)表示一条训练样本的特征值，y(i)表示一条训练样本的标签值

 - 缺点   遇到噪声值会导致陷入局部最优解

• 小批量梯度下降算法

  • 每次从训练集上随机抽取一个小样本,再抽取的小样本集上采取FG迭代更新权重

![在这里插入图片描述](https://img-blog.csdnimg.cn/20191211213950135.png)

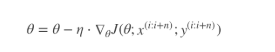
• 随机平均梯度下降算法(SAG)

  • 随机平均梯度算法克服了这个问题，在内存中为每一个样本都维护一个旧的梯度，随机选择第i个样本来更新此样本的梯度，其他样本的梯度保持不变，然后求得所有梯度的平均值，进而更新了参数

4. 欠拟合和过拟合

   欠拟合: 学习的模型太少, 再训练集和测试机都不能出现很好的你和

   过拟合: 学习的模型太多,再训练集上面比其他假设有很好的你和,但是在测试集却出现很大的误差

   • 欠拟合的解决办法 数据的特征过少

     • 添加其他特征项
       • 因为学习的特征太少 , 所以继续学习
     • 添加多项式特征
       • 例如在线性模型中通过调高高次项,使模型泛化能力变强

   • 过拟合的解决办法 学习的数据特征太多了

     • 重新清洗数据 可能是某些数据不纯
     • 增大数据的训练量 因为可能是训练的数据太小但是我们选择的特征占了这些训练的数据的很大一部分
     • 正则化
     • 减少特征的维度, 防止为灾难

   • 正则化

     
     

     • 我们要么删除高次项 要么让这些高次项的系数趋近0 使之变小
     • L1正则化
       • 使之系数直接为0, 删除这些高次项的特征带来的影响
       • LASSO回归
     • L2正则化
       • 作用:可以使得其中的系数趋近0 削弱某个特征的影响
       • 有点: 越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象
       • Ridge回归 (岭回归)

   • 弹性网络

     弹性网络在岭回归和LASSO回归进行了折中,通过混合比来进行控制

​

 - r=0：弹性网络变为岭回归
 - r=1：弹性网络便为Lasso回归

• from sklearn.externals import joblib

  模型的保存和加载

  • 保存：joblib.dump(estimator, ‘test.pkl’)
  • 加载：estimator = joblib.load(‘test.pkl’)